j1|中科大何力新教授：当量子力学遇见AI——深度学习在超算平台上模拟量子多体问题( 三 )

文章插图

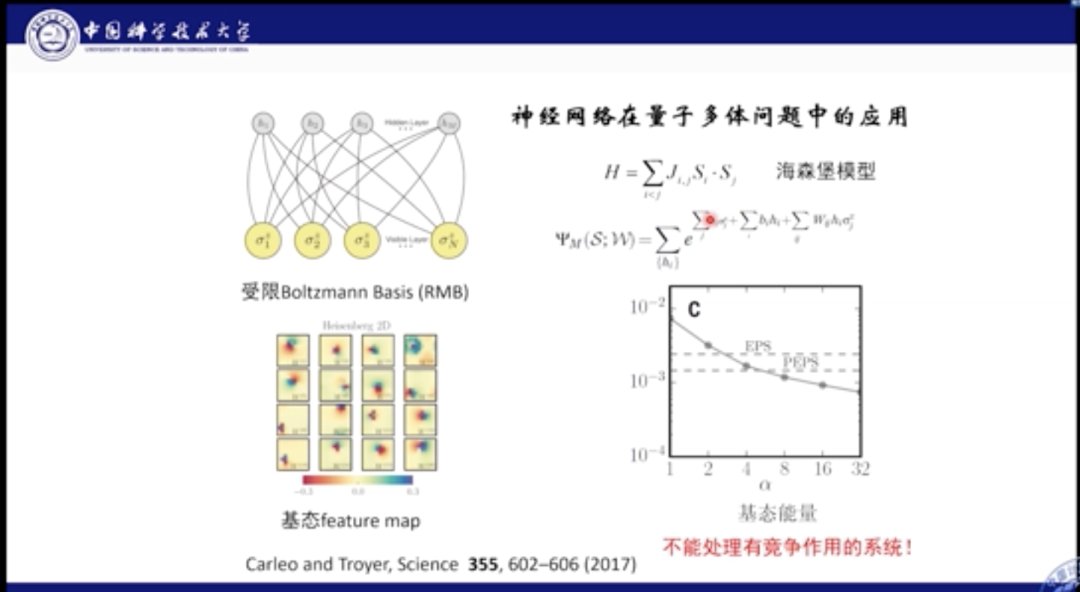
大家也在尝试将深度学习和机器学习用在量子多体问题中。上图是2017年的一篇Science工作，它使用受限玻尔兹曼机模型研究海森堡自旋模型，将系统的粒子波函数利用玻尔兹曼机进行表示和学习，通过优化系统的能量，得到神经网络的最佳参数。
在量子多体系统中，算法的好坏判断标准是计算的能量是否最优。从结果中我们看到，该计算能量的精度已经到达10^-3量级，甚至超过了（我们神威工作）之前PEPS的算法效果。
但是该神经网络也面临一些问题，它只能描述简单的物理模型，无法模拟具有竞争相互作用的物理系统。

人工智能的多体问题挑战

j1|中科大何力新教授：当量子力学遇见AI——深度学习在超算平台上模拟量子多体问题

文章插图

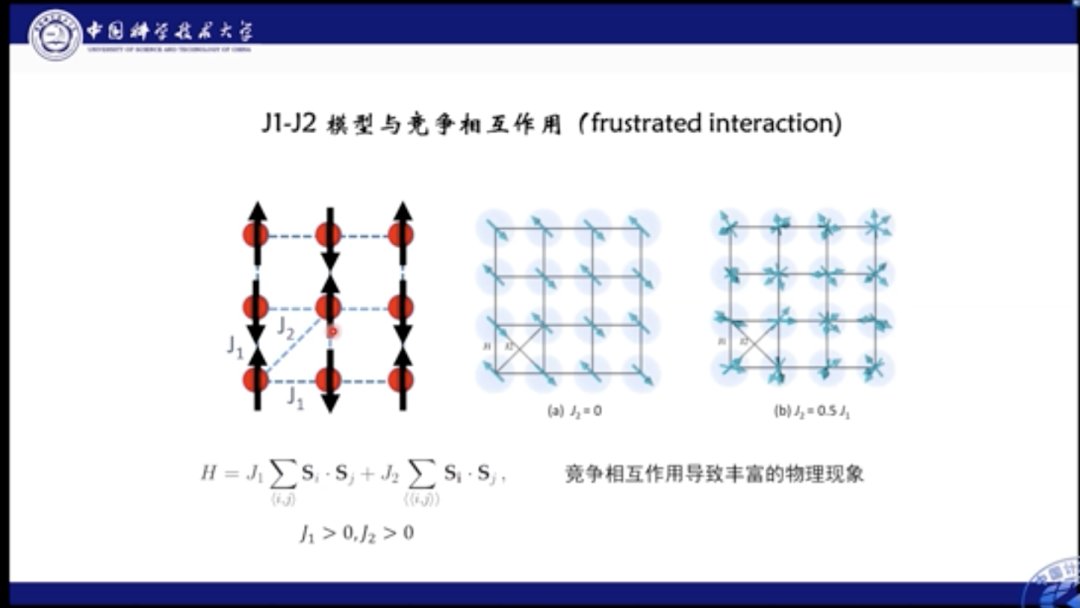
那么什么是相互竞争作用呢？我们结合这里的模型进行解释。J1－J2模型是一个典型的具有竞争相互作用的自旋模型。我们看到图中每个格点上有一个自旋，它们与近邻的自旋有相互作用，其中J1描述两个最近临的格点上的自旋相互作用，J2则描述了两个次近邻格点上自旋的相互作用，也就是对角线上的相互作用。如果相互作用的J大于0，则意味着这两个格点的自旋都倾向反平行。当J1, J2 都大于0时就会出现问题，即如果近邻格点是反平行，那么次近邻格点就一定是平行的，这就和J2相互作用的要求矛盾。该种带有竞争相互作用的系统被称为阻挫系统。

文章插图

打个比方，一个员工可能有两个老板，其中一个老板要求你向东走，另一个要求向西走。则此时会产生矛盾（Frustrated Interaction）。当然，如果其中一个老板很强势，我们跟着强势的走。但是如果两个老板势均力敌，你就会很迷茫。

文章插图

对J1-J2模型也是如此，如果J1较为强势，那么系统中的自旋会倾向于做出棋盘形状的持续排列。如果J2更强势，自旋则会沿对角线进行反平行排列。当两者相互作用效果相近时，则会产生更多丰富的物理现象。
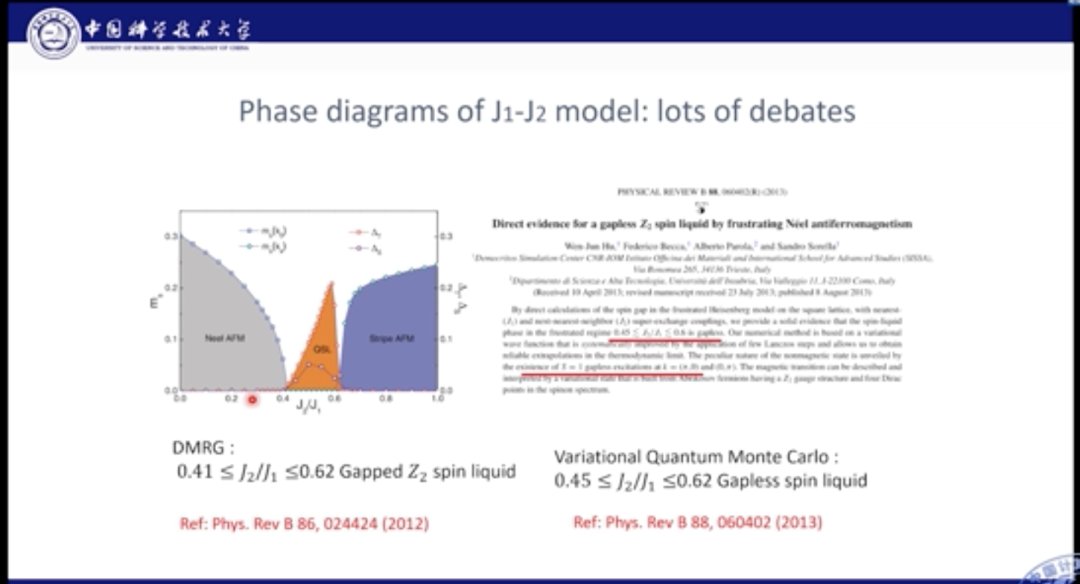
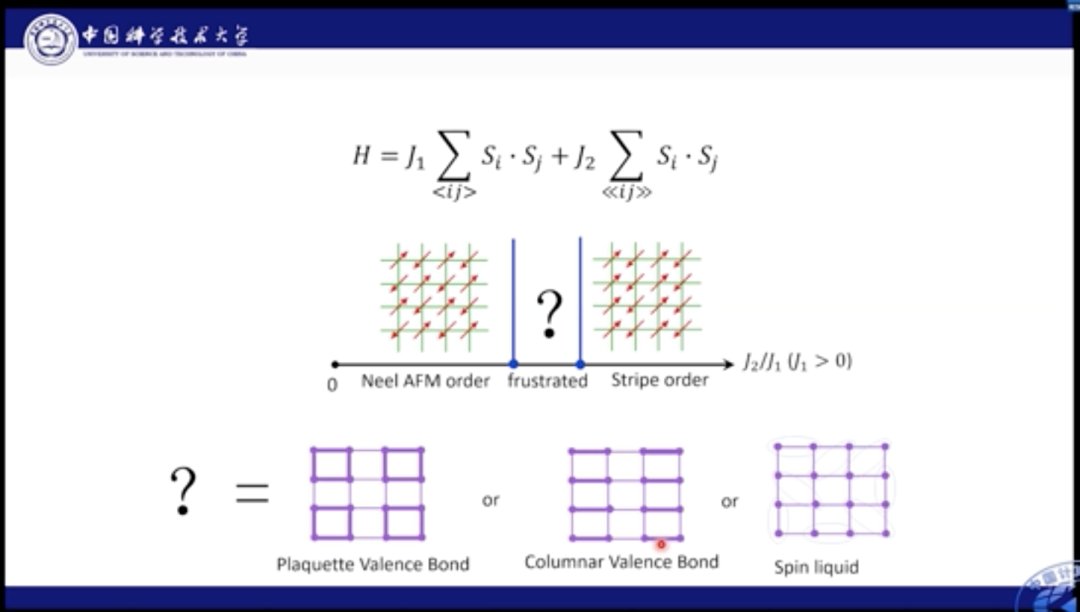
J1-J2模型十分经典，人们对其基态进行了长期的研究。目前针对J1较强，以及J2较强的情况研究已经较为清晰的结论，但是对于J1-J2共同作用的中间区域，一直存在争议。

文章插图

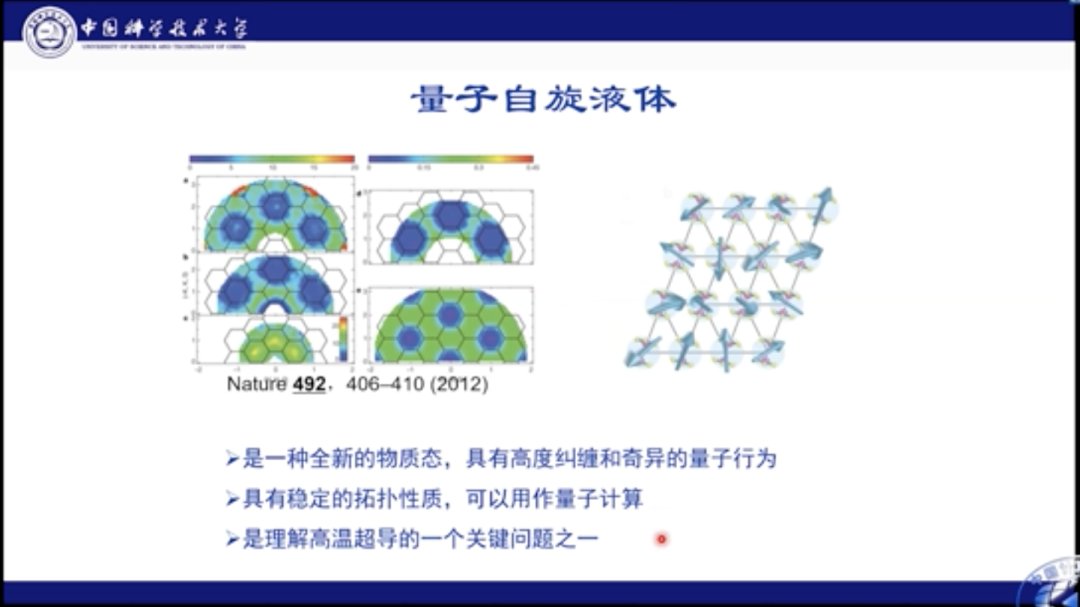
对于该区域的基态，人们有几种不同的看法。比如，有人认为格点可以形成Plaguette态，Plaguette态是一个规则有序的态；此外，也可能会形成Columnar态；也有人提出，可能其中就是一种混乱无序的状态，即自旋液体态。自旋液体态十分复杂，有着非常复杂的量子纠缠和奇异量子行为。Philip Anderson认为量子自旋液体是研究高温超导的关键问题之一。

深度学习和量子多体

文章插图

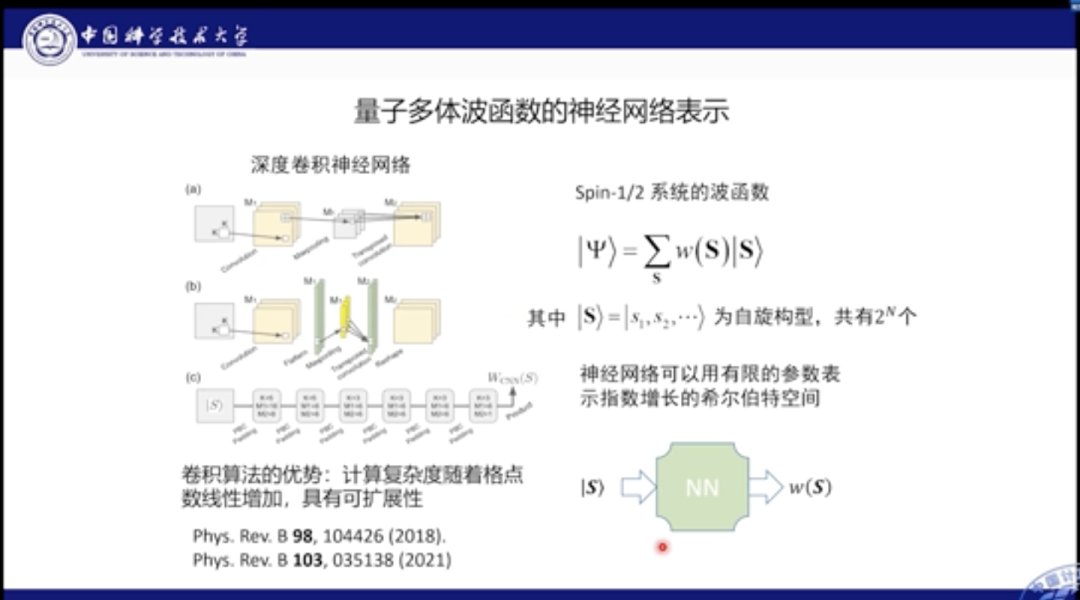
之前的玻尔兹曼机模型是无法很好地模拟该场景的。在该方法中，它将波函数视作所有可能自旋结构的叠加，其中W(S)就是自旋构型的权重，该权重在海森堡模型中都是>0的，但是在有竞争的模型中正负都有可能。因此在玻尔兹曼机模型中，就无法处理此类同时具有正负情况的波函数。
为此，我们提出使用深度卷积神经网络来描述波函数。我们的网络包括了很多Building Block，每个Block又分为多种算子，包括卷积、Max pooling和反卷积等。
当我们输入一个自旋构型，该网络可以给出有正有负的构型权重，此时的参数量是随格点数量线性增长，而非灾难的指数形增长，这就意味着我们的神经网络可以使用有限扩增的参数量来模拟出系统中指数增长的Hilbert空间。当然这个空间也是仅在基态附近的部分。

文章插图

当我们确定了神经网络的结构来模拟波函数后，重要的是需要获得系统的基态，所谓基态是指系统的能量最低态。也就是我们需要通过神经网络求解系统能量最低态的参数。
这里的能量可以表示成所有自旋构型加权求和的形式，因此可以使用马尔可夫抽样的方式进行求解。这是一个典型的强化学习场景，我们可以通过优化系统能量来得到网络参数。