2月6日12时,《张朝阳的物理课》第二十六期开播。搜狐创始人、董事局主席兼CEO张朝阳坐镇搜狐视频直播间,开讲谐振子模型的量子化问题。张朝阳先回顾经典力学中谐振子的运动方程、势能,再从双原子分子中两个原子间的势能出发,通过泰勒展开得到最低势能点附近的谐振子近似,以此阐述了谐振子在微观世界的普遍性,最后通过求解谐振子的薛定谔方程,带领网友成功理解谐振子模型的量子化问题。

文章插图
“人生的意义在于干活。”张朝阳在小白板上写下“虎年第二课”,同时为网友送上虎年祝福,他说,“干活需要学习,有了知识,才能更有效地干活。学物理,可以了解世界。”他也介绍,已有很多物理学家来搜狐视频开讲,“短视频时代,有心学习,除了看直播,还可反复看回放。”
回顾经典线性谐振子:胡克定律与运动方程张朝阳先带着网友回顾经典力学中的谐振子问题。以弹簧-小球模型为例,在经典力学中,谐振子的回复力是F=-kx,即所谓的胡克定律。根据牛顿第二运动定律,可以得到谐振子的运动方程:
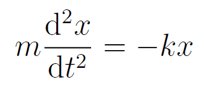
文章插图
他告诉网友,在通常的处理中,物理学家会通过定义角频率ω0=√(k/m)来简化符号的使用。他快速给出上述方程的解的形式:x=Re[x0 e^(iω0 t)]。他提醒说,“谐振子以正弦的形式振动,ω0是振动的角频率。”他也顺势介绍谐振子在振动过程中,动能和势能互相转化,总能量保持不变。在谐振子中,势能的微分du=-Fdx,于是得出谐振子的势能公式。
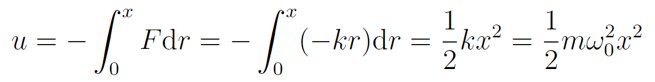
文章插图
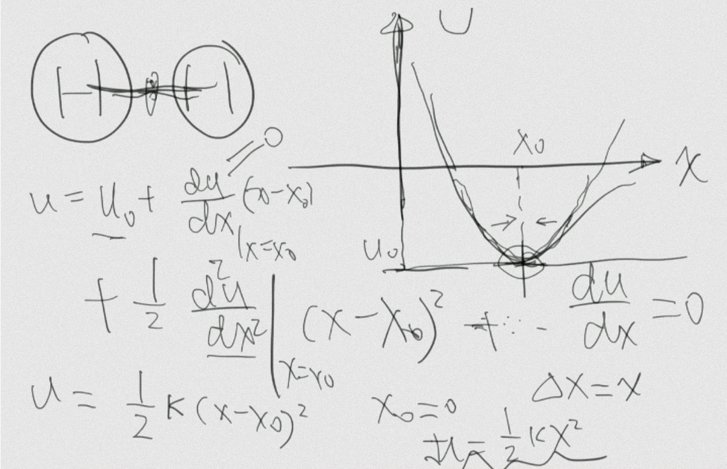
分子势能模型:选取平衡位置点 泰勒展开做近似谐振子是弹簧的理想模型,但是微观世界并没有弹簧,那么谐振子对于量子力学有什么意义呢?张朝阳以双原子分子为例,对此作出生动的介绍。他在小白板上明示双原子分子中的两个原子之间的势能。
文章插图
(双原子分子中的两个原子之间的势能曲线(右上角))
他说,“这个势能曲线有一个最低点。”从经典力学来看,当系统能量比较小时,双原子分子将会处在最低能处附近。而势能曲线在势能最低的形状恰好和抛物线类似,因此可以近似成谐振子。对此,张朝阳带着网友进行公式推导,主要方法来自于势能在能量最低点的泰勒展开:
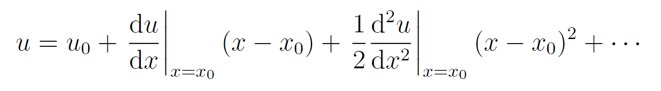
文章插图
【 薛定谔方程|《张朝阳的物理课》探究谐振子模型的量子化问题】他提醒网友,“省略号表示泰勒展开的高阶项,可忽略。”他还指出,在势能最低点,势能的一次导数为0,于是上式的一次项为0。把二阶导数记为k,重新定义势能零点和坐标原点,即可以把势能近似为谐振子势能的形式:
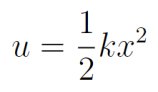
文章插图
“谐振子在物理中显得特别重要”,张朝阳强调了这个结论的普遍性。总的来说,只要是考虑势能极小值附近的微扰问题,都可以近似为谐振子。
求解薛定谔方程:谐振子能级与波函数提到谐振子的哈密顿算符,张朝阳再列公式做推导。
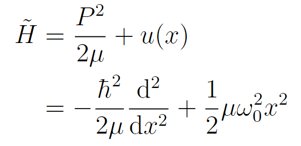
文章插图
“μ是等效质量”,他说,处理氢原子的时候由于质子比电子重很多,质子可以近似为在质心系中静止,因此哈密顿量可以直接用电子质量m。但是对于双原子分子,分子间的质量相差不大,哈密顿量里边的质量不能再直接使用其中某个原子的质量。
“有了谐振子的哈密顿量之后,就可以直接写出定态薛定谔方程了。”他告诉网友。
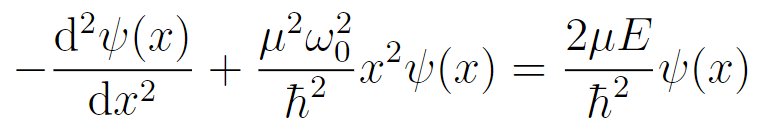
文章插图

文章插图
(张朝阳讲解谐振子的薛定谔方程)
于是,张朝阳作了变量代换:
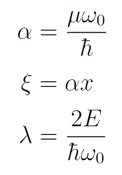
文章插图
将薛定谔方程化简为:
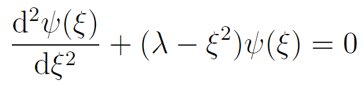
文章插图
他边推导边介绍,解此类方程在前面的课程已经进行过很多次了。为了进一步简化上述方程,需考虑当ξ趋向于无穷大时,这个方程近似为:
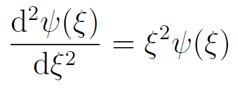
- 双原子|《张朝阳的物理课》气体比热随温而变?探究双原子分子比热问题
- 全球财经网|《2021DDoS攻击态势报告》|DDoS混合攻击大幅增长,较2020年增长80.8%
- 全球财经网|《网络空间测绘年报》|从安全事件透析网络空间资产安全热门风险点
- 光刻机供应商 ASML:欢迎并大力支持《欧洲芯片法案》
- deep|Nature封面:人类又输给了AI,这次是玩《GT赛车》游戏
- 百家号|「千寻数藏」正式发布运营,山海经《瞳》系列火热开售
- 侵权|抖音:侵权《长津湖》为不实信息
- Netflix|Netflix低调神作,洗钱版《绝命毒师》
- 超级马里奥|别具创意玩趣!高玩打造3D全息版《超级玛丽》
- 菜鸟的python笔记|《菜鸟的python笔记》是python初学者的福音
